Assignment Solution
Minimum Cost flow is a technique of diminishing the cost compulsory to deliver extreme volume of flow conceivable in the network. It is found that an addition of extreme flow problem with the additional constraint on flow cost for every edge. The main difference in minimum cost flow with respect to the normal max flow is the source and destination or sink have a certain bound on the restrictions on the flow.
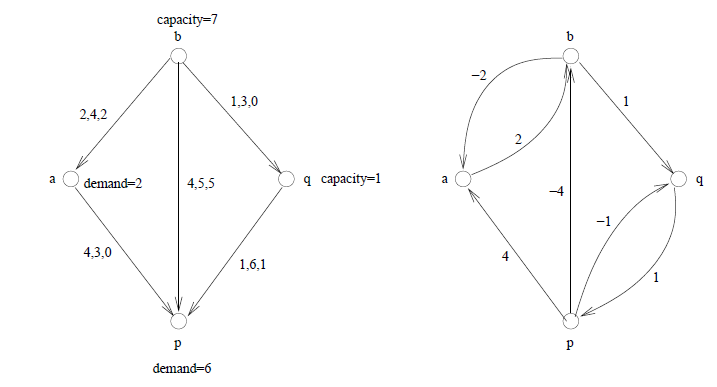
The example based on minimum cost flow is discussed below
Let’s consider the diagraph which is G = (V, E) in which each edge is having capacity e and the unit cost is c.
Each vertex is having he demand which is termed as b (v).
If b (v)>0 then the vertex is called the sink otherwise the vertex is called the source
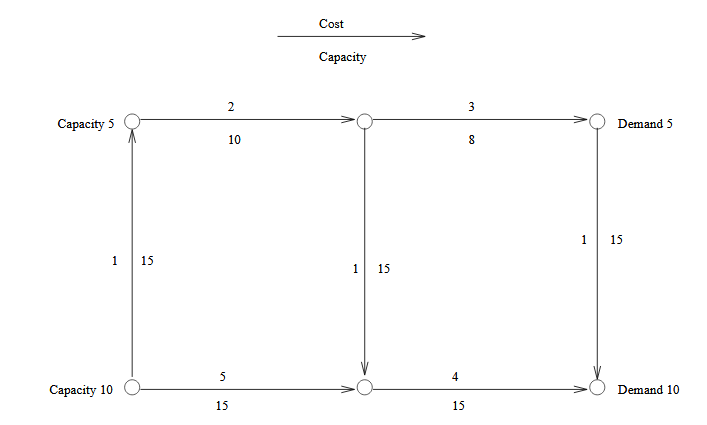
The minimum cost problem deals in supplying the sinks from the sources using the flow in the efficient manner such that the objective function defined as
The dual variables having the balanced equations are denoted as yv where v belongs to V and having the capacity constraints which are denoted as Zvw € E
Then the Rc = Cvw + yv -yw
Where Rc is the reduced cost for the edge (v, w) and therefore - Cvw - yv + yw <= Zvw which is equivalent to - Rc<= Zvw
Now the question arises when is the set of feasible solutions (x,y and z) are optimal?
The optimal solution is
If Ue is not equal to the positive infinity and Ze must be zero and Ze>=- Rc must hold. The Z has the negative coefficient in the objective function so the efficient choice for the z is as small as possible Ze = max{0,- Rc}
It can be shown below with the help of the residual graph in which if the supply at a particular source node and the demand at a particular sink node are simultaneously reduced by one unit